Case description - Digital Freepen

If you arrived directly on this page from a link, visit the introduction and table of contents.

This section describes :

The rules of the particular problem the neural networks are trying to solve.
The structure of the 'controller' neural network.
The input/output interface used by the neural network.

Rules of the influence game

The Influence Game (created for the purpose of this project) is inspired from the ancient board game Go: its goal is to obtain as much territory as possible and to capture enemy units. Just like in Go, the rules are simple, but finding a good solution can be difficult. The reason is that strategies require balance. More territory can be obtained by spreading out, but spreading out too much will weaken the formation of units and potentially lead to a collapse.

The game was also designed to be able to expect a reasonable learning rate from a small neural network such that its error function is smooth. By error function we mean a function that maps the space S of possible moves into real numbers representing the quality of that move. Let M be an optimal move in a given situation and let E(N) be the error function representing the quality of a move N relative to M such that e(M) = 0 and e(N) >= 0 for all moves N. The goal of an ANN is then to find small local minima of E(N) by improving incrementally.

It is easier to find the minimize a smooth error function. In games such as Chess or Go, the difference between two possible adjacent positions for a move is often the difference between losing and winning. That leads to large fluctuations within the error function. In contrast, in a game such as Backgammon, having a piece in column X instead of column X + 1 is rarely game breaking. That leaves a margin of error which has allowed ANNs to be much more successful at playing Backgammon than Chess³. In the Influence Game, there is a large enough margin of error so that the ANN can evolve towards smaller error values in a reasonable amount of time.

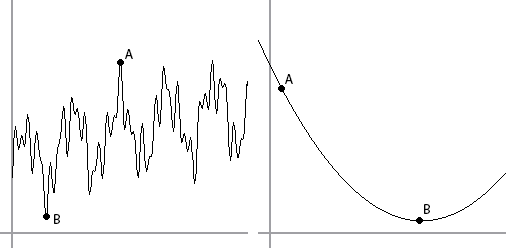
A demonstration of rough (left) vs smooth (right) error functions. Starting from some initial move A, it is easier to find minima in the function when the function is smooth.

Without further ado, the rules of the Influence Game :

An instance of the game is referred to as a match.
A match is played on a 180x180 grid, referred to as the field.
In every given match, two teams play against each other : a positive team (red) and a negative team (blue). Similarly to electrical charges, there is no advantage in being positive or negative : they are opposite but equivalent.
Each team is comprised of 21 identical players.
Players on each team start on opposites side of the field and are arranged symmetrically.
Each player generates a circular influence aura of radius 25.
An aura modifies the value of the field in its radius. The effect decreases with distance*. The aura of positive players increase the value of the field and the aura of negative players decrease the value of the field. Overlapping auras can stack (they are added up).
If a positive player finds himself in a spot where the field has negative value smaller than -1.0, he is removed from the game, along with its aura.
Similarly, if a negative player finds himself in a spot where the field has positive value greater than 1.0, he is removed from the game, along with its aura.
The game is played for 250 time steps.
During each time step, every player can move by one unit in one of the eight adjacent tiles.
When the game ends, points are assigned to each team and the team with the most points wins. The number of points assigned to the positive team is equal to the number of cells with value strictly greater than zero. Similarly the number of points assigned to the negative team is equal to the number of cells with value strictly smaller than zero. It is important to notice that we are counting how much area is covered by the player's aura and not the total values of the field cells. This gives a benefit to spreading out.

* The strength of an aura is evaluated with the function
\[ strength = \sqrt{1 - (distance / radius)^{2}} \]

The video below demonstrates a few sample Influence Games, with commentary.

It is possible for both teams to have the same number of points. In those cases, neither team is considered to have won. In practice, this situation usually only occurs with first-generation teams, when no player on either team moves during the match, which is not a desired behavior.

ANN controller structure

A simple feed-forward artificial neural network model is used in the project. This model is simple to understand and is sufficient for our purposes. We will provide a very simple description here; there are excellent external sources that can provide more detailed explanations of the concept of artificial neural networks.

A set of numerical inputs with range [-1, 1] is used as input for neurons of the input layer. The input layer is fully connected to a layer of hidden neurons which, in turn, is fully connected to a layer of output neurons. The input layer and the hidden layer also have an additional bias neuron.

Given the inputs from layer K, the ith neuron on layer K + 1 will have have output :
\[ o_{i} = T(\displaystyle\sum\limits_{j\in K} {w_{ij}o_{j}+b_{j}}) \] where
\[ w_{ij} = weight~from~neuron~j~to~i \] \[ o_{j} = output~of~neuron~j~on~layer~K \] \[ b_{K} = bias~neuron~on~layer~K \]

and where T is the threshold sigmoid function defined as :
\[ T(x)=\dfrac{1}{1+e^{(-2x)}} \]

Each team is defined by a single ANN. It determines the movements of each individual player separately. Since this project is also about self-organizing systems, the inputs for the ANN will depend on the state of each individual player and not the playing field as a whole. For example, a player can measure the value of the field at a relative distance X away from him but not the value of the field at an absolute point P on the field, such as the upper-left corner. In other words, there is no central command post - a player only see and acts according to its surroundings.

Input/Output interface

The ability of a player to analyze its environment is limited to the amount of information it has available. Thus, the choice of input sensors are crucial in the ANN's decision-making capabilities and will determine the behavior of the team as a whole. The standard input set for this project consists of 14 normalized inputs as follow :

Distance from closest border (horizontal)
Distance from closest border (vertical)
Inverse of distance from closest teammate (horizontal)
Inverse of distance from closest teammate (vertical)
Inverse of distance from closest enemy (horizontal)
Inverse of distance from closest enemy (vertical)
to 14. Values of the field at a distance X in the Forward, Forward-Left,Left, Backward-Left, Backward, Backward-Right, Right, Forward-Right directions

These input sensors allow a player to get basic information to interact with other players, allies or opponents. A larger number of input neurons would allow more complex decision making, but introduce more complexity than necessary here.

The output sensors are very simple, given the rules of the game. The player can either stand still or move in one of 8 directions. There are two output neurons : one for horizontal movement, one for vertical movement. If the output is below a certain threshold, the player will move left or down, respectively. If the output is above a certain threshold, the player will move right or up.

Given our standard I/O interface for ANNs, we define the ANN of every team to have 1 hidden layer, 14 neurons in the input layer, 14 neurons in the hidden layer and 2 neurons in the output layer. With the bias neurons, every ANN therefore contains (14 + 1) * 14 + (14 + 1) * 2 = 240 connections between neurons and the same amount of weights.

We should also note the importance of programming symmetry into each Influence Game match. By symmetry we mean that each input and output sensor that measures a parameter in a given direction measures it in the direction relative to the player. As an example, for sensor 9, a player will measure the value of the field to "its left" and not the value "in the direction of the left side of the field".

If we were to use the latter case, early ANNs would be confused when they switch sides of the field. While it is possible for an ANN to evolve in a way such that it will have acceptable behavior regardless of which side of the field it starts on, it will involve a larger number of generations to reach the same result, possibly by a large factor.

The next section will deal with training artificial neural networks to exhibit interesting behavior.